Sometimes developers face optimization challenges in their code — regardless of the programming language they use. One of the most common optimization challenges is the complexity (or performance) of an algorithm that increases and grows infinitely when the number of arguments it has to process increases. This is called big-O complexity or big-O notation.
In this blog post, you’ll learn how to perform DataWeave code optimization to improve performance by following the big-O notation principles.
Common DataWeave enrichment
Let’s assume we have to combine two data sets to generate the final result which we want to be returned by the message transformer event processor.
The first data set has been received from the backend with a collection of possible flight destinations.

Next to this data, we have a static collection of details about all airports based on their IATA (International Air Transport Association) code which uniquely defines all the airport’s details: full airport name, location, coordinates, etc.
| openFlightsAirportId | 492 | 499 | 502 |
| airportName | London Luton Airport | Jersey Airport | London Gatwick Airport |
| city | London | Jersey | London |
| country | United Kingdom | Jersey | United Kingdom |
| IATA | LTN | JER | LGW |
| ICAO | EGGW | EGJJ | EGKK |
| longitude | 51.87469864 | 49.207901 | 51.14810181 |
| latitudeAltitude | -0.368333012 | -2.195509911 | -0.190277994 |
| timeZone | 526 | 277 | 202 |
| DST | 0 | 0 | 0 |
| timeZone | E | E | E |
| type | Europe/London | Europe/Jersey | Europe/London |
| source | airport | airport | airport |
Our task is to add IATA details to every flight received from the backend and generate a final JSON response.
Classic DataWeave approach
The classical approach would be to store the entire IATA collection in a variable and insert the corresponding airport information field into the resulting collection using standard DataWeave. This means using the map operator to iterate over the collection of records and add an extra key:value pair to every flight object where the value is the corresponding IATA details. The find operator is used to locate the proper entry in the IATA collection.
%dw 2.0
output application/json
var airportInfo = readUrl("classpath://airportInfoTiny.csv","application/csv" )
---
payload map {
($),
airportInfo: (airportInfo filter (e,i) -> e.IATA == $.destination)[0]
}
Fig 3: Classic approach to mapping data
This fragment of code reads the IATA information into the variable airportInfo,then using the map operator it iteratively traverses the payload, which is a collection of flights (see fig 1), and adds a new key:value pair to the end of every flight. The object is taken from the airportInfo variable where filter is used to locate an IATA field matching the destination field from the flight object.
The output of this code we will be integrated flight and airport data:

The issue with the classic approach
This transformation looks straight forward, but let’s think about the operational effort which is needed to process it:
- The map operator iterates through the collection and a new key:value pair added to every object where the find operator has to be executed.
- Then the find operator performs a lookup in the airportInfo collection and iterates through every field of every object to locate an IATA key matching the destination key.
So, every time we are looking through the airportInfo variable we have to perform a full scan of every key:value pair to detect a matching object. In this case, the number of iterations will be (n * m) where n is a number of flight objects and m is an amount of key:value pairs in the airportInfo variable. The Big-O notation comes into play and shows us how complexity will increase with the number of objects. The complexity increase will be quadratic O(n2).
Optimized DataWeave approach
DataWeave has the capability to improve the performance of this iterative process significantly by using a functional programming approach where one of the concepts gives the variable similar functionality as a function. Within variable creation, a functional definition can be used.
%dw 2.0
output application/json
var airportInfo =
readUrl("classpath://airportInfoTiny.csv","application/csv" )
groupBy $.IATA
---
airportInfo
Fig 5: Group the airport information be IATA code
Output from this code would be as shown below:

Now we have all objects grouped by the IATA code, thus the IATA code acts as a unique identifier.
After modifications, our final code will be the following:
%dw 2.0
output application/json
var airportInfo = readUrl("classpath://airportInfoTiny.csv","application/csv" )
groupBy $.IATA
---
payload map {
($),
airportInfo: airportInfo[$.destination][0]
}
Fig 7. Optimized approach
Certainly, there will not be any changes to the final output results however, complexity will be heavily reduced as we are not performing any global lookups and can select top-level IATA keys from the airportInfo variable which becomes hashmaps after groping. It makes our complexity O(n) where n is the number of flight objects.
Conclusion
In this blog post, we’ve seen just one of many optimization examples which can be coded with DataWeave.
The graph below shows different dependencies between big-O complexity and execution time.
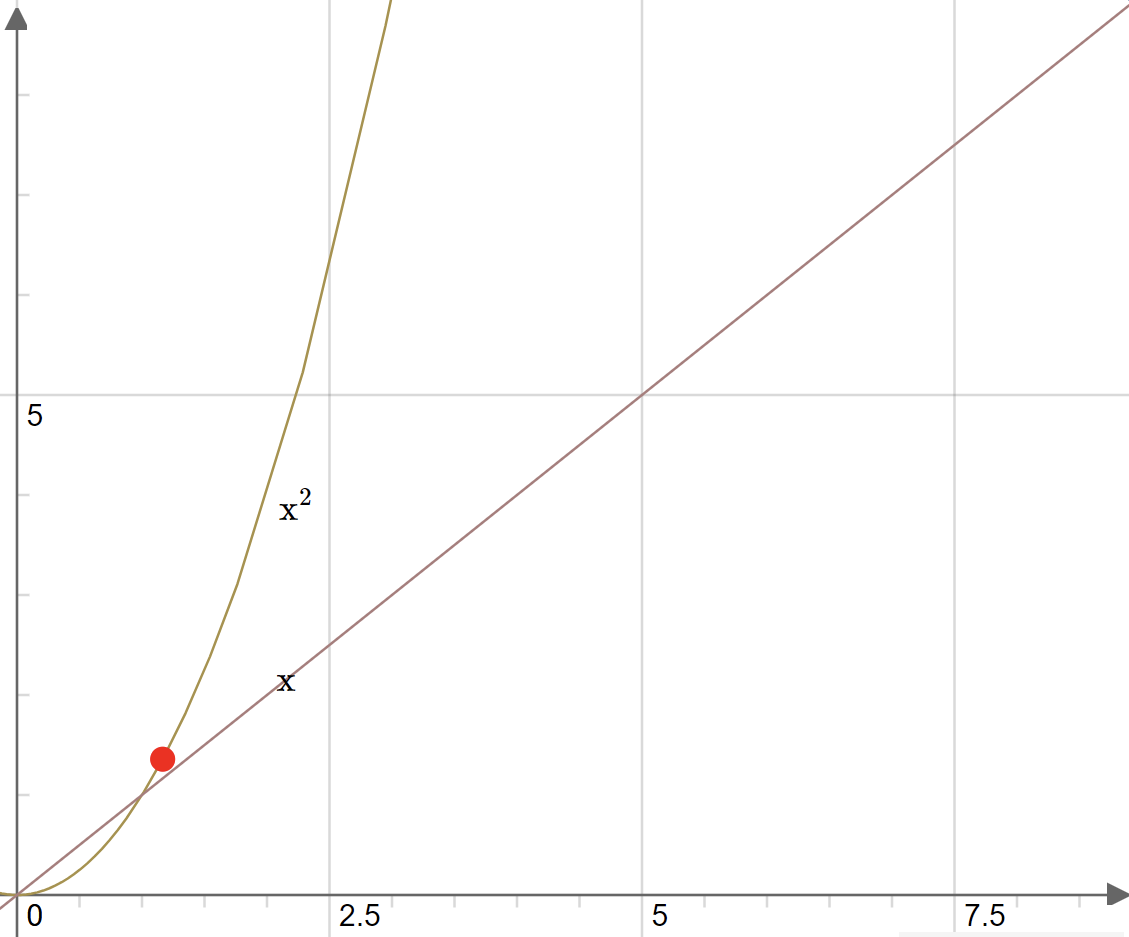
We managed to reduce complexity from O(n2) down to O(n) which brings a significant performance improvement.
There are many more best practices demonstrated in the MuleSoft DataWeave class available online or in the classroom. Please check our training website for availability and information about our developer and architecture classes.